ECUACIONES IRRACIONALES

En mi opinión este tipo de ecuaciones son muy sencillas, puesto que lo único que tenemos que hacer es elevar al cuadrado ambos miembros de la ecuación para así poder despejar las raíces cuadradas.

Y después de habernos deshecho de las raíces lo único que tenemos que hacer es igualar a cero, pasando todos los términos a un mismo miembro, y así poder quedarnos con una ecuación de segundo grado que resolveremos mediante la fórmula.

ECUACIONES BICUADRADAS

Una ecuación bicuadrada es aquella que toma forma de: ax^4 +bx^2 +c=0

Para resolver este tipo de ecuaciones lo primero que debemos hacer es llamar a x^2 de otra manera, en este caso lo llamaremos p, y por lo tanto nos quedará que ax^4+bx+c=0 es lo mismo que; p^2+p+c=0 , es decir que nos quedará una ecuación de segundo grado que tendremos que resolver .

finalmente, para terminar de resolver este tipo de ecuaciones, al obtener las dos raices lo que tenemos que hacer es obtener las raices cuadradas de cada una de ellas, puesto que lo que hemos llamado p en un principio es realmente x^2, y así lo que conseguiremos es que se nos vaya el cuadrado y obtengamos el valor de x.

ecuaciones de segundo grado

En este apartado hablaremos de las ecuaciones de segundo grado,es imprescindible que no se den por vencidos y que si no lo entienden lo lean tantas veces como sea necesario puesto que con perseverancia y trabajo todo se consigue.

Bueno, dicho esto empezamos con ecuaciones de segundo grado.

Para resolver una ecuación de segundo grado existen dos maneras, la primera es por el método de factorización , que es el más utilizadoy la segunda es por la odiada fórmula de resolución de ecuaciones de segundo grado.

Antes de hacer nada les voy a explicar que es factorizar.

Factorizar es la expresión de un número o polinomio como el producto de números primos o polinomios más sencillos.

Así podemos decir que:

35=7×5 ; 325=5^2×13 ; 35X^2=7X×5X ; 325y^3=(5y)^2×13y

Para factorizar nos debemos preguntar siempre en orden lo siguiente:

• ¿se puede sacar factor común?

• ¿Es una identidad notable?

• Si no se puede realizar ninguno de los métodos anteriores precederemos a utilizar el método de ruffini o a extraer todas las raíces del polinomio.

En el caso de que se pueda sacar factor común procederemos, para identificarlo solo tendremos que fijarnos de si en el polinomio hay algún factor que se repite, ya que este método consiste en extraer el monomio que se repite y colocarlo fuera metiendo todo lo demás en un paréntesis.Así:

En el caso de que no se pueda sacar factor común tendremos que identificar si es una identidad notable,pero;

¿QUÉ SON LAS IDENTIDADES NOTABLES?

Las identidades notables son una serie de igualdades que siempre van a seguir una regla fija,  para poder identificarlas debemos sabernos estas tres fórmulas:

1.CUADRADO DE UNA SUMA.

2.CUADRADO DE UNA DIFERENCIA.

3.PRODUCTO DE DOS TÉRMINOS CONJUGADOS.

Y tan sólo ver si coincide nuestro polinomio con alguna de sus estructuras, posteriormente, tan sólo debemos sustituir.

En el caso de que nuestro polinomio no se pueda factorizar de ninguna de las maneras anteriores, lo haremos con el método de Ruffini y para ello debemos seguir los siguientes pasos:

1. Lo primero que tenemos que hacer es obtener todos los divisores del término independiente, tanto positivos como negativos.
2. Luego debemos proceder a ordenar de mayor a menor grado el polinomio, dejando un hueco en blanco en caso de que no exista el término del grado correspondiente.
3. Hecho esto, comenzaremos a hacer ruffini, como ya he explicado(pinchad en "rufini" arriba del todo) pero, en este caso , el numerito que pondremos a la izquierda del esquema, será el divisor que estemos probando.
4. Al obtener el resto, nos debería de dar cero si es una raíz del polinomio, y en el caso contrario no lo es.

En el caso de que nos resulte más fácil o no podamos factorizar utilizaremos la siguiente fórmula, que consistirá en sustituir.

ECUACIONES DE PRIMER GRADO

Para resolver una ecuación de primer grado

1.Quitamos denominadores, multiplicando por el m.c.m.

2.Quitamos paréntesis.

3.Transponemos términos pasando las "x" a un miembro y los números a otro.

4.Simplificamos los términos semejantes

5.Despejamos la incógnita.

6.Comprobamos la solución.

DEFINICIÓN DE ECUACIÓN

Una ecuación es una igualdad entre dos expresiones algebraicas que se verifica sólo para determinados valores de las variables.

-Dos ecuaciones con las mismas soluciones se dice que son semejantes.

Si tenemos la incógnita sola en un miembro y el resto en el otro, se dice que está despejada.

El proceso que paso a paso nos lleva por ecuaciones equivalentes hasta tener la incógnita se llama resolver una ecuación.

REGLAS DE LA SUMA Y EL PRODUCTO

Regla de la suma: consiste en sumar o restar la misma expresión a los dos miembros de la igualdad.

Regla del producto: Multiplicar o dividir los dos miembros de la igualdad por una misma expresión distinta de cero.

-La regla de la suma nos permite pasar lo que está sumando en un miembro al otro restando y viceversa.

-La regla del producto nos permite pasar lo que está a un lado multiplicando, dividiendo y viceversa.

FRACCIONES ALGEBRAICAS

-Una fracción algebraica F(x) es un cociente en el que el numerador A(x) y el denominador B(x) son dos polinomios.

Se dice que dos fracciones algebraicas son equivalentes cuando los productos cruzados coinciden.

SON EQUIVALENTES PORQUE: (x+2)·(x-2)=x^2-4 ·1 =

                                        x^2-4 =x^2-4

                         

EL MÁXIMO COMÚN DIVISOR Y EL MÍNIMO COMÚN MULTIPLO

-Una vez obtenida la descomposición de dos o más polinomios, el máximo común divisor es el producto de los factores comunes con exponente menor.

Y,por otro lado, el mínimo común múltiplo será el producto de los factores comunes y no comunes con exponente mayor.

TEOREMA DEL RESTO

El resto de la división de un polinomio P(x) entre un divisor (x-a) es igual al valor numérico del polinomio cuando x=a , y se indica como P(a).

valor numérico de un polinomio

valor numérico
Se le llama valor numérico de un polinomio P(x) cuando "x" vale "a" y se representa por P(a) al valor numérico que se obtiene al sustituir en el polinomio la variable "x" por el valor "a".

-Se dice que el valor "a" es una raíz del polinomio P(x) si el valor numérico del polinomio para x=a es 0

"a" es una raíz de P(x)<->P(a)=0

división de polinomios

DIVISIÓN DE POLINOMIOS

-Para dividir dos polinomios, se disponen los términos del dividendo y del divisor como si de una división numérica se tratara, dejando en el dividendo espacios en blanco en los grados que no tienen término. Se divide el monomio mayor del dividendo con el monomio mayor del divisor y el resultado se coloca en el cociente.

Se multiplica este valor por los distintos términos del divisor y se restan del dividendo.

Luego, se repite el proceso hasta que en el resto el grado sea inferior al del divisor.

DIVISIÓN POR EL MÉTODO DE RUFFINI

1. -La división por el método de ruffini sólo puede realizarse si el divisor es de la forma(x-a)donde "a" es un número real. Si sucede que el divisor es (x+a) ,se aplica : x+a=x-(-a)
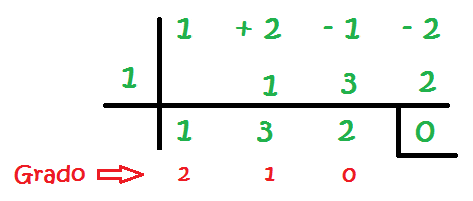
2. Se disponen todos los coeficientes del dividendo,  p(x) y el término independiente del divisor "a" cambiado de signo en una tabla como esta:
3. 
4. Se multiplica el primer coeficiente del dividendo por el valor de "a" y se coloca el resultado en la columna siguiente
5. 
6. se suman los valores de la columna siguiente y se repite el proceso,hasta realizar la suma de la última columna-el último término obtenido corresponde al resto de la división y el resto de los coeficientes corresponden al polinomio cociente de un grado inferior al del dividendo.

suma y resta de polinomios

DOS POLINOMIOS SON SEMEJANTES CUANDO TIENEN LA MISMA PARTE LITERAL.
-Para sumar dos polinomios ,se suman los coeficientes de los monomios semejantes , y la parte literal se queda intacta.
Por ejemplo:
   15x^6 -2x^4             +7x^2        +18
              +9x^4 -8x^3 +15x^2 +9x -3
+15x^6 +7x^4 -8x^3 +22x^2 +9x +15
-Para restar dos polinomios, se suma al minuendo el opuesto del sustraendo, 

Por ejemplo:
 15x^6  -2x^4             +7x^2         +18
             -9x^4   +8x^3 -15x^2 -9x +3
+15x^6 -11x^4 -8x^3   -8x^2 -9x +21

Definición de polinomio

Bueno chicos , vamos a plantearnos la pregunta del siglo, "¿qué es un polinomio?"

Un polinomio es la suma, resta, división, multiplicación,etc, de dos o más monomios de distinto grado.

-Para tenerlo claro os digo de entrada que se denomina grado de un polinomio al mayor  exponente de las incógnitas o variables.
término

-Y de paso os digo que el independiente es el término que no va a acompañado de ninguna variable.